3.9 Derivatives of General Exponential and Logarithmic Functions
Recall that in the conceptual insight box in section 3.2.2. we discussed the meaning of \(b^x\). We will now give the derivative of the function \(f(x)=b^x\) for any real number \(b>0\).
THEOREM 1 Derivative of \(f(x) = b^x\)
\[\boxed{\dfrac{d}{dx}b^x = (\ln b)b^x\text{ for }b>0}\tag{1}\]
For example, \((10^{x})' = (\ln 10)10^{x}\).
Proof of Theorem 1
The proof follows from the chain rule after observing that every exponential function \(y=b^x\) where \(b >0\) can be rewritten in terms of base \(e\) as follows.
\[b^x=\left(e^{\ln b}\right)^x=e^{x \ln b}\]
Since now \(f(x)=b^x\) is rewritten a s a composition of differentiable functions, it is differentiable by the chain rule, and, using the chain rule, we get a formula for its derivative:
\[\frac{d}{dx} b^x=\frac{d}{dx}e^{x \ln b}= e^{x \ln b} \frac{d}{dx}(x \ln b)=e^{x \ln b} (\ln b)= (\ln b) b^x\]
EXAMPLE 1
Differentiate: (a) \(f(x) = 4^{3x}\) and (b) \(f(x) = 5^{x^2}\).
Solution
(a) The function \(f(x) = 4^{3x}\) is a composite of \(4^{u}\) and \(u = 3x\):
\[\frac{d}{dx}4^{3x} = \left(\frac{d}{du}4^u\right)\frac{du}{dx} = (\ln 4)4^u(3x)' = (\ln 4)4^{3x}(3)= (3\ln 4)4^{3x}\]
(b) The function \(f(x)=5^{x^2}\) is a composite of \(5^{u}\) and \(u = x^{2}\):
\[\frac{d}{dx}5^{x^2} = \left(\frac{d}{du}5^u\right)\frac{du}{dx} = (\ln 5)5^u(x^2)' = (\ln 5)5^{x^2}(2x)= (2\ln 5)x5^{x^2}\]
We have already shown in Section 3.2 that the derivative of \(\ln x\) is \(\displaystyle \frac{1}{x}\). We state it here once again as a theorem.
183
THEOREM 2 Derivative of the Natural Logarithm
\[\boxed{\dfrac{d}{dx}\ln x = \frac{1}{x}\text{ for }x>0}\tag{2}\]
EXAMPLE 2
The two most important calculus facts about exponentials and logs are
\[\boxed{\frac{d}{dx}e^x = e^x\text{ and }\frac{d}{dx}\ln x = \frac{1}{x}}\]
Differentiate: (a) \(y = x \ln x\) and (b) \(y = (\ln x)^{2}\).
Solution
(a) Use the Product Rule:
\begin{align*} \frac{d}{dx}(x\ln x) &=x\cdot(\ln x)' + (x)'\cdot\ln x\\ &=x\cdot\frac{1}{x} + \ln x = 1 + \ln x \end{align*}
(b) Use the General Power Rule:
\[\frac{d}{dx}(\ln x)^2 = 2\ln x \cdot \frac{d}{dx}\ln x = \frac{2\ln x}{x}\]
In Section 3.7, we proved the Power Rule for whole-number exponents. We can now prove it for all exponents \(n\) by writing \(x^{n}\) as an exponential and using the Chain Rule. For \(x > 0\),
\begin{align*} x^n&= (e^{\ln x})^{n} = e^{n\ln x}\\[5pt] \frac{d}{dx}x^n&=\frac{d}{dx}e^{n\ln x}\\[5pt] &= \left(\frac{d}{dx}n\ln x\right)e^{n\ln x}\\[5pt] &=\left(\frac{n}{x}\right)x^n = n x^{n-1} \end{align*}
We obtain a useful formula for the derivative of \(\ln (f(x))\) by applying the Chain Rule with \(u = f(x)\):
\[\frac{d}{dx}\ln(f(x)) = \frac{d}{du}\ln u\frac{du}{dx} = \frac{1}{u}\cdot u' = \frac{1}{f(x)}f'(x)\]
\[\boxed{\dfrac{d}{dx}\ln(f(x))=\dfrac{f'(x)}{f(x)}}\tag{3}\]
EXAMPLE 3
Differentiate: (a) \(y = \ln(x^{3} + 1)\) and (b) \(y=\ln(\sqrt{\sin x})\).
Solution Use Eq. (3):
(a)\[\frac{d}{dx}\ln(x^3+1) = \frac{(x^3+1)'}{x^3+1} = \frac{3x^2}{x^3+1}\]
(b) The algebra is simpler if we write \(\ln(\sqrt{\sin x})= \ln\left((\sin x)^{1/2}\right) = \frac{1}{2}\ln(\sin{x})\):
\begin{align*} \frac{d}{dx}\ln(\sqrt{\sin x}) &= \frac{1}{2}\frac{d}{dx}\ln(\sin x) \\ &=\frac{1}{2}\frac{(\sin x)'}{\sin x} = \frac{1}{2}\frac{\cos x}{\sin x} = \frac{1}{2}\cot x \end{align*}
EXAMPLE 4 Logarithm to Another Base
Calculate \(\frac{d}{dx}\log_{10}x\).
 REMINDER According to Eq. (1) in Section 1.6, we have the “change-of-base” formulas
REMINDER According to Eq. (1) in Section 1.6, we have the “change-of-base” formulas
\[\boxed{\log_bx=\frac{\log_ax}{\log_ab} \text{ and } \log_bx = \frac{\ln x}{ln b}}\]
Solution By the change-of-base formula (see margin), \(\log_{10}x = \frac{\ln x}{\ln10}\). Therefore,
\[\frac{d}{dx}\log_{10}x = \frac{d}{dx}\left(\frac{\ln x}{\ln10}\right) = \frac{1}{\ln10}\frac{d}{dx}\ln x = \frac{1}{(\ln10)x}\]
It follows, as in Example 4, that for any base \(b > 0, b \neq 1\):, we can find the derivative in a similar manner and obtain the following theorem:
THEOREM 3 Derivative of \(f(x)= \log_b x \)
\[\boxed{\dfrac{d}{dx}\log_bx = \frac{1}{(\ln b)x}\text{ for }x>0 \text{ and } b>0} \tag{4}\]
Question 3.22 Derivatives of General Exponential Functions Progress Check 1
Find \(f'(x)\) for \(f(x)= \log_2 x\)
| A. |
| B. |
| C. |
| D. |
The next example illustrates logarithmic differentiation. This technique saves work when the function is a product or quotient with several factors.
184
EXAMPLE 5 Logarithmic Differentiation
Find the derivative of
\[f(x) = \frac{(x+1)^2(2x^2 - 3)}{\sqrt{x^2 + 1}}\]
Solution In logarithmic differentiation, we differentiate \(\ln (f(x))\) rather than \(f(x)\) itself. First, expand \(\ln(f(x))\) using the logarithm rules:
\begin{align*} \ln(f(x))&=\ln\left((x+1)^2\right) + \ln(2x^2 - 3) - \ln(\sqrt{x^2+1})\\ &=2\ln(x+1) + \ln(2x^2 - 3) - \frac{1}{2}\ln(x^2+1) \end{align*}
Then use Eq.(3):
\begin{align*} \frac{f'(x)}{f(x)} &= \frac{d}{dx}\ln(f(x)) = 2\frac{d}{dx}\ln(x+1) + \frac{d}{dx}\ln(2x^2 - 3) - \frac{1}{2}\frac{d}{dx}\ln(x^2+1)\\ \frac{f'(x)}{f(x)} &=\frac{2}{x+1} + \frac{4x}{2x^2-3} - \frac{x}{x^2+1} \end{align*}
Finally, multiply through by \(f(x)\):
\[f'(x) = \left(\frac{2}{x+1} + \frac{4x}{2x^2-3} - \frac{x}{x^2+1}\right)\left(\frac{(x+1)^2(2x^2 - 3)}{\sqrt{x^2 + 1}}\right)\]
EXAMPLE 6
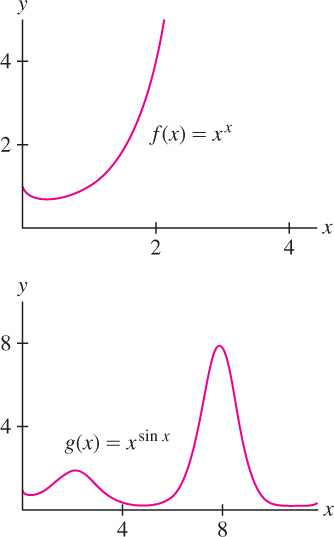
Differentiate (for \(x > 0\)): (a) \(f(x) = x^{x}\) and (b) \(g(x) = x^{\sin x}\).
Solution The two problems are similar (Figure 3.51). We illustrate two different methods.
(a) Method 1: Since \(x>0\), we can use the identity \(x = e^{\ln x}\) to rewrite \(f(x)\) as an exponential:
\begin{align*} f(x)&=x^x = (e^{\ln x})^{x} = e^{x\ln x}\\[5pt] f'(x)&= (x\ln x)' e^{x\ln x}= (1+\ln x)e^{x\ln x} = (1+\ln x)x^x \end{align*}
(b) Method 2: Apply Eq. (3) to \(\ln (g(x))\). Since \(\ln(g(x)) = \ln(x^{\sin x}) = (\sin x) \ln x\),
\begin{align*} \frac{g'(x)}{g(x)} &= \frac{d}{dx}\ln(g(x))=\frac{d}{dx}\left((\sin x)\ln x\right) = \frac{\sin x}{x} + (\cos x)\ln x \\[5pt] g'(x)&=\left(\frac{\sin x}{x} + (\cos x)\ln x\right)g(x) = \left(\frac{\sin x}{x} + (\cos x)\ln x\right)x^{\sin x} \end{align*}
Question 3.23 Derivatives of General Exponential Functions Progress Check 2
Assume \(x>0\). Find \( \displaystyle \left.\frac{d}{dx} x^{e^x}\right|_{ x=1} \)
| A. |
| B. |
| C. |
| D. |
3.9.1 The Hyperbolic Trigonometric Functions and their Derivatives
The hyperbolic functions are certain special combinations of \(e^{x}\) and \({e}^{-x}\) that play a role in engineering and physics (see Figure 3.52 for a real-life example). The hyperbolic sine and cosine, often called or pronounced “cinch” and “cosh,” are defined as follows:
\[ \boxed{\sinh x=\frac{e^x - e^{-x}}{2},\quad \cosh x = \frac{e^x+e^{-x}}{2}} \]

As the terminology suggests, there are similarities between the hyperbolic and trigonometric functions. Here are some examples:
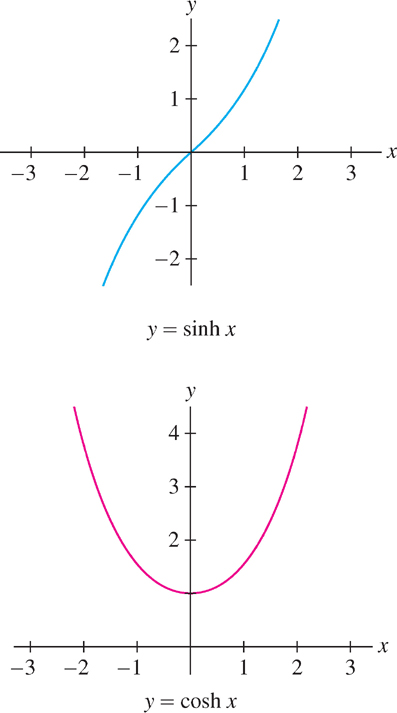
- Parity: The trigonometric functions and their hyperbolic analogs have the same parity. Thus, \(\sin x\) and \(\sinh x\) are both odd, and \(\cos x\) and \(\cosh x\) are both even (see Figure 3.54): \[ \sinh(-x)=-\sinh x,\quad \cosh (-x) = \cosh x \]
- Identities: The basic trigonometric identity \(\sin^{2}x + \cos^{2}x = 1\) has a hyperbolic analog: \[ \cosh^2x-\sinh^2x=1\tag{2} \]
48
The addition formulas satisfied by \(\sin \theta\) and \(\cos \theta\) also have hyperbolic analogs:
\[ \boxed{\begin{array}{rl} \sinh(x+y)&=\sinh x\cosh y + \cosh x \sinh y\\ \cosh(x+y)&=\cosh x\cosh y + \sinh x \sinh y \end{array}} \]
- Hyperbola instead of the circle: Because of the identity \(\sinh^{2}t - \cosh^{2}t = 1\), the point \((\cosh t, \sinh t)\) lies on the hyperbola \(x^{2} - y^{2} = 1\), just as \((\cos t, \sin t)\) lies on the unit circle \(x^{2} + y^{2} = 1\) (Figure 3.53).
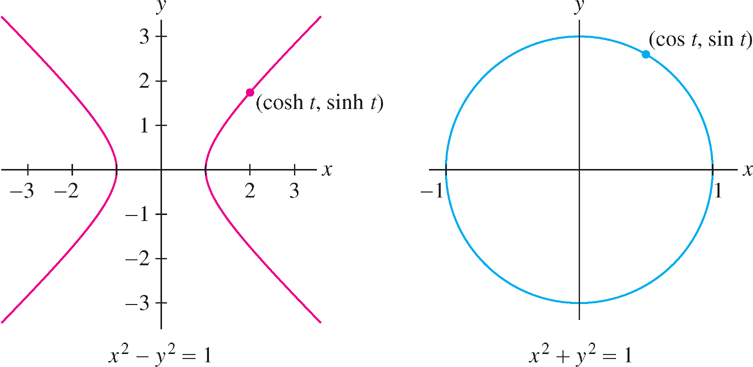
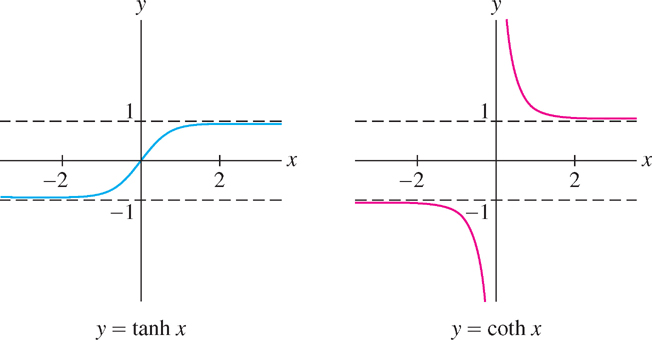
- Other hyperbolic functions: The hyperbolic tangent, secant, cotangent, and cosecant functions (see Figure 3.55 and Figure 3.56) are defined like their trigonometric counterparts: \[ \boxed{\begin{array}{rl} \tanh x=\frac{\sinh x}{\cosh x}=\frac{e^x - e^{-x}}{e^x + e^{-x}} & \mbox{sech} \ x =\frac{1}{\cosh x}= \frac{2}{e^x+e^{-x}}\\ \mbox{coth} \ x=\frac{\cosh x}{\sinh x}=\frac{e^x + e^{-x}}{e^x - e^{-x}} & \mbox{csch} \ x =\frac{1}{\sinh x}= \frac{2}{e^x-e^{-x}} \end{array}} \]
Below are the graphs of these functions. Note that these graphs have no similarity to the graphs of the corresponding trigonometric functions. For instance, they are not periodic.

Here are the graphs of the hyperbolic tangent and cotangent (Figure 3.56). Observe that these have the same horizontal asymptotes \(y=-1\) and \(y=1\) but have disjoint range.
EXAMPLE 7 Verifying the Basic Identity
Verify Eq. (2): \(\cosh^{2}x - \sinh^{2}x = 1\).
Solution Because \(\cosh x=\frac{1}{2}(e^x+e^{-x})\) and \(\sinh x=\frac{1}{2}(e^x-e^{-x})\), we have
\[ \cosh x + \sinh x = e^x,\quad \cosh x - \sinh x = e^{-x} \]
We obtain Eq. (2) by multiplying these two equations together:
\[ \cosh^2x-\sinh^2x=(\cosh x+\sinh x)(\cosh x - \sinh x)= e^x\cdot e^{-x}=1 \]
49
Since the hyperbolic trigonometric functions are special combinations of \(e^{x}\) and \(e^{-x}\), the formulas for their derivatives are readily obtained. It turns out that the derivatives of the hyperbolic trigonometric functions are once again similar to those for the corresponding trigonometric functions, differing at most by a sign.
Consider the hyperbolic sine and cosine:
\[\sinh x = \frac{e^x - e^{-x}}{2} \text{ and } \cosh x = \frac{e^x + e^{-x}}{2}\]
Their derivatives are
\[\boxed{\dfrac{d}{dx}\sinh x =\cosh x}\quad\text{and}\quad\boxed{\dfrac{d}{dx}\cosh x = \sinh x}\]
185
We can check this directly. For example,
\[\frac{d}{dx}\sinh x = \frac{d}{dx}\left(\frac{e^x - e^{-x}}{2}\right) = \frac{e^x + e^{-x}}{2} = \cosh x\]
Note the resemblance to the formulas \(\frac{d}{dx}\sin x = \cos x\), \(\frac{d}{dx}\cos x = -\sin x\). The derivatives of the other hyperbolic functions, which are computed in a similar fashion, also differ from their trigonometric counterparts by a sign at most.
Derivatives of Hyperbolic Trigonometric and Trigonometric Functions
\begin{align*} \frac{d}{dx}\tanh x &=\mathrm{sech}^2\,x &\frac{d}{dx}\tan x &=\mathrm{sec}^2\,x \\[5pt] \frac{d}{dx}\coth x &= -\mathrm{csch}^2\,x &\frac{d}{dx}\cot x &= -\mathrm{csc}^2\,x\\[5pt] \frac{d}{dx}\mathrm{sech}\,x &=-\mathrm{sech}\,x \tanh x &\frac{d}{dx}\mathrm{sec}\,x &=\mathrm{sec}\, x \tan x\\[5pt] \frac{d}{dx}\mathrm{csch}\,x &= -\mathrm{csch}\,x\coth x&\frac{d}{dx}\mathrm{csc}\,x &= -\mathrm{csc}\,x\cot x \end{align*}
EXAMPLE 8
 REMINDER Hyperbolic sine and cosine satisfy the basic identity (Section 3.11):
REMINDER Hyperbolic sine and cosine satisfy the basic identity (Section 3.11):
\[\cosh^2 x - \sinh^2 x = 1\]
Verify: \(\frac{d}{dx}\coth x = -\mathrm{csch}^2\,x\).
Solution By the Quotient Rule and the identity \(\cosh^2 x - \sinh^2 x = 1\),
\begin{align*} \frac{d}{dx}\coth x &= \left(\frac{\cosh x}{\sinh x}\right)' = \frac{(\sinh x)(\cosh x)' - (\cosh x)(\sinh x)'}{\sinh^2x}\\[5pt] &=\frac{\sinh^2x - \cosh^2x}{\sinh^2x} = \frac{-1}{\sinh^2x} = -\mathrm{csch}^2\,x \end{align*}
EXAMPLE 9
Calculate: (a) \(\frac{d}{dx}\cosh(3x^2+1)\) and (b) \(\frac{d}{dx}\sinh x\tanh x\)
Solution
(a) By the Chain Rule, \(\frac{d}{dx}\cosh(3x^2+1) = 6x\sinh(3x^2+1)\).
(b) By the Product Rule,
\[\frac{d}{dx}(\sinh x\tanh x) = \sinh x\:\mathrm{sech}^2\,x + \tanh x\cosh x = \mathrm{sech}\,x\tanh x + \sinh x\]
Question 3.24 Derivatives of General Exponential Functions Progress Check 3
Find the derivative of the function \(f(x) = \cosh (x) \cdot \cos (2x)\)
| A. |
| B. |
| C. |
| D. |
3.9.2 Inverse Hyperbolic Trigonometric Functions
Recall that a function \(f(x)\) with domain \(D\) has an inverse if it is one-to-one on \(D\). Each of the hyperbolic functions except \(\cosh x\) and \(\mathrm{sech}\,x\) is one-to-one on its domain and therefore has a well-defined inverse. The functions \(\cosh x\) and \(\mathrm{sech}\,x\) are one-to-one on the restricted domain \(\{x : x \geq 0\}\). We let \(\cosh^{-1}x\) and \(\mathrm{sech}^{-1}\,x\) denote the corresponding inverses (Figure 3.57). In reading the following table, keep in mind that the domain of the inverse is equal to the range of the function.

186
Inverse Hyperbolic Trigonometric Functions and Their Derivatives
 REMINDER The derivatives of \(\cosh^{-1}x\) and \(\mathrm{sech}^{-1}\,x\) are undefined at the endpoint \(x = 1 \) of their domains.
REMINDER The derivatives of \(\cosh^{-1}x\) and \(\mathrm{sech}^{-1}\,x\) are undefined at the endpoint \(x = 1 \) of their domains.
\[ \begin{array}{ccc} \hline \text{Function}&\qquad\text{Domain}\qquad&\text{Derivative}\\ \hline &&\\ \begin{array}{rl} \vphantom{\frac{1}{\sqrt{x^2+1}}}y &\hspace{-10pt}\hspace{4mu}=\sinh^{-1}x\\[5pt] \vphantom{\frac{1}{\sqrt{x^2+1}}}y &\hspace{-10pt}\hspace{4mu}=\cosh^{-1}x\\[5pt] \vphantom{\frac{1}{1 - x^2}}y &\hspace{-10pt}\hspace{4mu}=\tanh^{-1}x\\[5pt] \vphantom{\frac{1}{1 - x^2}}y &\hspace{-10pt}\hspace{4mu}=\coth^{-1}x\\[5pt] \vphantom{\frac{1}{x\sqrt{1 - x^2}}}y &\hspace{-10pt}\hspace{4mu}=\mathrm{sech}^{-1}x\\[5pt] \vphantom{\frac{1}{|x|\sqrt{x^2+1}}}y &\hspace{-10pt}\hspace{4mu}=\mathrm{csch}^{-1}x \end{array} & \begin{array}{c} \vphantom{\frac{1}{\sqrt{x^2+1}}}\text{all }x\\[5pt] \vphantom{\frac{1}{\sqrt{x^2+1}}}x\geq 1\\[5pt] \vphantom{\frac{1}{1 - x^2}}|x| < 1\\[5pt] \vphantom{\frac{1}{1 - x^2}}|x|>1\\[5pt] \vphantom{\frac{1}{x\sqrt{1 - x^2}}}0<x\leq 1\\[5pt] \vphantom{\frac{1}{|x|\sqrt{x^2+1}}}x\neq 0 \end{array} &\begin{array}{rl} \frac{d}{dx}\sinh^{-1}x&\hspace{-10pt}\hspace{4mu}=\frac{1}{\sqrt{x^2+1}}\\[5pt] \frac{d}{dx}\cosh^{-1}x&\hspace{-10pt}\hspace{4mu}=\frac{1}{\sqrt{x^2-1}}\\[5pt] \frac{d}{dx}\tanh^{-1}x&\hspace{-10pt}\hspace{4mu}=\frac{1}{1 - x^2}\\[5pt] \frac{d}{dx}\coth^{-1}x&\hspace{-10pt}\hspace{4mu}=\frac{1}{1 - x^2}\\[5pt] \frac{d}{dx}\mathrm{sech}^{-1}x&\hspace{-10pt}\hspace{4mu}=-\frac{1}{x\sqrt{1 - x^2}}\\[5pt] \frac{d}{dx}\mathrm{csch}^{-1}x&\hspace{-10pt}\hspace{4mu}=-\frac{1}{|x|\sqrt{x^2+1}} \end{array}\\ &&\\ \hline \end{array} \]
EXAMPLE 10
Verify: \(\displaystyle \frac{d}{dx}\tanh^{-1}x = \frac{1}{1-x^2}\).
Solution We first note that \(1- \tanh^2 x = \mathrm{sech}^2 x\). This follows from the formula \(\cosh^2 x - \sinh^2 x=1\), by dividing through by \(\cosh^2 x\). Now apply the formula for the derivative of an inverse. We do this in the Leibniz notation version [Eq. (2) in Section 3.8].
From \(y= \tanh^{-1}(x)\) we get \(x= \tanh y\) and differentiating this gives \(\displaystyle \frac{dx}{dy}=\mathrm{sech}^2 y\). Therefore
\[\displaystyle \frac{dy}{dx}=\frac{1}{\large \frac{dx}{dy}}=\frac{1}{\mathrm{sech}^2 y}= \frac{1}{1- \tanh^2 y}=\frac{1}{1-x^2}\]
This gives the desired result:
\[\frac{d}{dx}\tanh^{-1}x = \frac{1}{1-x^2}\]
The functions \(y = \tanh^{-1}x\) and \(y = \coth^{-1}x\) both have derivative \(\displaystyle \frac{1}{1-x^2}\). Note, however, that their domains are disjoint (Figure 3.58).

3.9.3 Section 3.9 Summary
- The hyperbolic sine and cosine: \[ \sinh x = \frac{e^{x}-e^{-x}}{2} \text{ (odd function)}, \quad\cosh x =\frac{e^x+e^{-x}}{2} \text{ (even function)}. \] The remaining hyperbolic functions: \[ \tanh x=\frac{\sinh x}{\cosh x},\quad \coth x=\frac{\cosh x}{\sinh x},\quad \text{sech}\,x=\frac{1}{\cosh x},\quad \text{csch}\,x=\frac{1}{\sinh x} \]
- Basic identity: \(\cosh^{2}x - \sinh^{2}x = 1\).
- The inverse hyperbolic functions and their domains:
| \(\sinh^{-1} x\), for all \(x\) | \(\coth^{-1} x\), for \(|x| > 1\) |
| \(\cosh^{-1} x\), for \(x \geq 1\) | \(\text{sech}^{-1} x\), for \(0 < x \leq 1\) |
| \(\tanh^{-1} x\), for \(|x| < 1\) | \(\text{csch}^{-1} x\), for \(x \neq 0\) |
- Derivative formulas for logarithmic and exponential functions:
\[\frac{d}{dx}e^x = e^x\quad\frac{d}{dx}\ln x=\frac{1}{x}\quad\frac{d}{dx}b^x = (\ln b) b^x\quad \frac{d}{dx}\log_bx=\frac{1}{(\ln b)x}\]
187
- Derivative formulas for hyperbolic trigonometric functions:
\begin{align*} \frac{d}{dx}\sinh x &=\cosh x &\frac{d}{dx}\cosh x &= \sinh x \\ \frac{d}{dx}\tanh x &=\mathrm{sech}^2\,x &\frac{d}{dx}\coth x &= -\mathrm{csch}^2\,x\\ \frac{d}{dx}\mathrm{sech}\,x &=-\mathrm{sech}\,\tanh x &\frac{d}{dx}\mathrm{csch}\,x &= -\mathrm{csch}\,x\coth x \end{align*}
- Derivative formulas for inverse hyperbolic trigonometric functions:
\begin{align*} \frac{d}{dx}\sinh^{-1} x &=\frac{1}{\sqrt{x^2+1}} &\frac{d}{dx}\cosh^{-1} x &= \frac{1}{\sqrt{x^2 - 1}} \quad(x>1) \\ \frac{d}{dx}\tanh^{-1} x &=\frac{1}{{1- x^2}}\quad (|x|<1) &\frac{d}{dx}\coth^{-1} x &= \frac{1}{{1- x^2}}\quad (|x|<1) \\ \frac{d}{dx}\mathrm{sech}^{-1}\,x &=-\frac{1}{x\sqrt{1-x^2}}\quad(0<x<1) &\frac{d}{dx}\mathrm{csch}^{-1}\,x &= -\frac{1}{|x|\sqrt{1+x^2}}\quad(x\neq0) \end{align*}